文章專區

Take Home Message
．李再鈐的低限雕塑作品〈元〉將數學算式「1的 n 次方等於 1」轉化為藝術哲學。
．該作品由八個正方體依序旋轉拼接，形成宛如 DNA 的螺旋結構。這種獨特造型讓雕塑能以雙平行邊的「W」字型穩固站立，像極了溜冰者帥氣的平衡姿態。
．宏偉的公共藝術也能化身掌中科學玩具。我們利用幾何解構與立體卡片原理，將鏤空長方體壓扁再展開，就能 DIY 成可摺疊的〈元〉模型。透過動手實作，讓原本抽象的雕塑變得親民，引領大眾在把玩之間，解開隱藏在低限藝術背後、數學與空間對話的創意奧義。

五行雕塑小集，是臺灣七〇年代相當重要的現代雕塑團體，由楊英風、李再鈐、朱銘等大師級人物組成。1986 年，五行雕塑小集推出第三波的聯展，李再鈐這回改以正方體為低限創作〔註〕的元素，變化出〈元〉、〈好合〉與〈虛實之間〉等造型迥異的雕塑（圖一）。多年後，〈元〉與〈虛實之間〉分別典藏於國立臺灣美術館（以下稱國美館）與高雄市立美術館（以下稱高美館）。

〔註〕低限藝術在 1960 年代於美國紐約興起，這種非寫實表達的一大重點，即是減少藝術家的情感表現，並朝單純、邏輯的選擇發展。

透過這篇文章，筆者將藉由簡易教具與動手操作的設計路徑，把〈元〉這件國美館典藏的公共藝術，解構成學生方便 DIY 的實做模型。再來，我們會進一步將 Pop Up 3D 立體卡片的驚奇概念融入其中，以期讀者在認識、把玩之餘，透過數學與藝術跨領域的創意交流和另類對話，充分感受李再鈐創作中「低限之所以為無限」的藝數密碼！

潛藏在 1ⁿ 裡的奧義

源自於西方的低限幾何造型雕塑，從東方《道德經》的「道生一，一生二，二生三，三生萬物」得到呼應。這回關於〈元〉的命名，或可由「一『元』復始，萬象更新」得到靈感。至於〈元〉的造型，李再鈐從正方形的面積算式 1²=1，聯想到正方體的體積算式 1³=1，進而推展到 n 維超體的 1ⁿ=1。正因如此，他取「造形之始」的正方體為「1」，同時賦予「色彩之始」的大紅色為畫面，由此規律地演變出「1ⁿ」的圖像。

李再鈐將 8 個全等的正方體，倆倆以正方形面對面拼接成〈元〉。過程中，2 個零件拼接成 1 個長方體，然後轉個直角拼接第 3 個零件，而在續轉直角拼接第 4 個零件時，整體還形成一個如同「右手比讚」的立體造型（圖二 ➀ ～ ➃ ）。仿此原則，繼續拼接剩餘的 4 個零件（ 圖二 ➄ ～ ➇ ），即可完成一個如 DNA 螺旋結構的〈元〉。

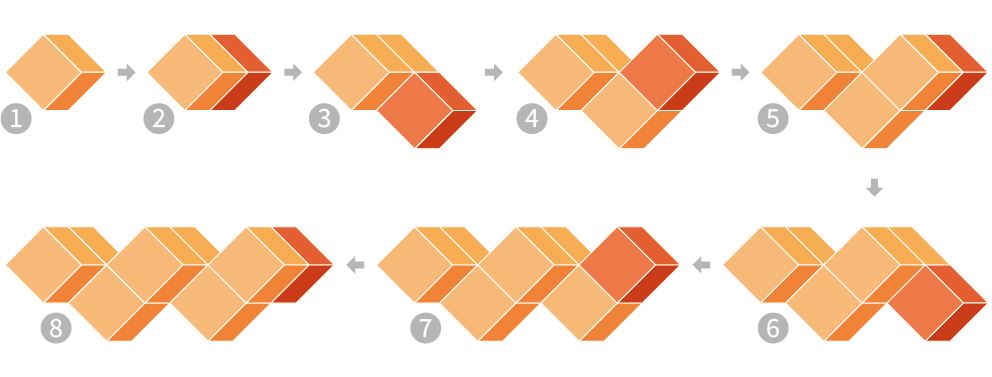
圖二｜〈元〉的低限元素與構成步驟側視分解圖

解構一件低限藝術的誕生

關於〈元〉的結構剖析，以下分別從它擺設的方位、零件的數量，以及零件的組成等面向逐一說明。

首先是擺放姿態。關於〈元〉的擺設方位，其實可以有很多種姿態。在拼接第四或第六個零件時

（圖二➃、➅），上方或下方會出現兩道互相平行的稜邊，以此為支撐可穩固整體的重心落點。而在拼接第七至八個零件時（圖二➆ ～➇），上方會出現共平面（即幾何形狀所落的同一平面）的第三道平行稜邊。雖也可以倒過來，以此穩固重心，但此時 M字型的「架勢」看起來不夠靈巧（圖三 ➀），所以李再鈐仍選定以兩道平行邊當底部。最終，〈元〉便以此款向上開展卻又四平八穩的W 字型的模樣，很帥氣地用一雙「冰刀」平行錯位的姿態擺 pose ！

再來是零件數量。當以低限零件展示〈元〉的無限架構時，為什麼正方體的數量需求是 8 個呢？若從重心的落點分析，當繼續拼接第 9 個零件，〈元〉的下方也會出現共平面的第三道平行稜邊（圖三 ➁ ），但此時重心早已穩固，有畫蛇添足之嫌。我們改從結構的觀點分析，8 個小正方體恰好可以拼組成一個更大的正方體（圖三 ➂ ），而這個數量上的特徵或許正呼應李再鈐當初發想造形之始的 1²=1、1³=1、……、1ⁿ=1。綜合上述可知，拼組〈元〉的正方體數量，多一個不巧、少一個不足，就是要 8 個恰恰好。……【更多內容請閱讀科學月刊第674期】