文章專區

Take Home Message
► 人工智慧其實就是要把問題化為一個「函數」，再利用各種機器學習、深度學習等方式，讓電腦想辦法學習這個函數。
► 透過One-Hot Encoding 編碼方式、Softmax 等轉換，我們可以讓AI 模型的函數處理結果更為精準。
► 設計損失函數便能幫AI 模型「評分」，使用方法是把訓練資料都輸入AI 模型中讓它作答，最後再看AI 模型和正確答案的差距。

隨著人工智慧（artificial intelligence, AI）技術興起，有愈來愈多人投入人工智慧領域的研究。人工智慧其實很簡單，首先就是要把問題化為一個「函數」。舉例來說，假設我們想做一個AI系統，辨識在臺灣常見的三種八哥，分別是臺灣原生種八哥（Acridotheres cristatellus，俗稱土八哥）、外來種白尾八哥（Acridotheres javanicus）、外來種家八哥（Acridotheres tristis）。化成函數的形式，就是由我們輸入一張八哥的照片，電腦輸出這是哪種八哥。

土八哥

（Noel Reynolds, CC BY 2.0, Wikimedia Commons）

白尾八哥
（JJ Harrison, CC BY-SA 4.0, Wikimedia Commons）

問題是，電腦只會處理數字，該怎麼告訴我們答案是「土八哥」呢？我們只需要改變一個方式，就是給每隻八哥一個編號！比方說土八哥是1號、白尾八哥是2號、家八哥是3號。

接著，我們就可以利用各種機器學習、深度學習等方式，去打造一臺「函數學習機」，讓電腦想辦法學會這個函數。如果採用深度學習，我們會需要大量的訓練資料：一種八哥大約需要1000 張照片，然後再用這些訓練資料去訓練我們的函數學習機（即AI模型）。如果AI模型學成了這個函數，那只要輸入一張八哥的照片，就會輸出一個數字，讓我們知道這是哪種八哥。

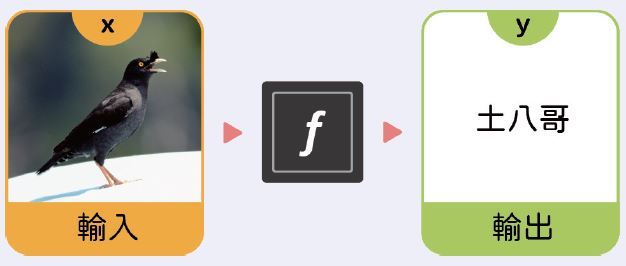
比如說，輸入一隻八哥的照片，輸出結果是1.2，我們就知道「啊，這是土八哥！」，因為數值1.2介於編號1 的土八哥與編號2 的白尾八哥之間，且較靠近 1。

One-Hot Encoding

目前這個函數看來還很美好，但問題是：如果我們輸入一張照片，AI模型告訴我們是2.5，這該怎麼解讀呢？難道要說我們的AI模型判斷，這隻鳥有50％的機會是編號2 的白尾八哥，另外50％的機會是編號3的家八哥嗎？如果你有認真看這三種八哥，就會發現土八哥其實和白尾八哥比較像，白尾八哥和家八哥反而不太像。依常理來說，應該不會有這種分不清的情況吧？

至於會發生這種問題的原因，出在我們給八哥的編號，就只是一個代號，並沒有本來數字系統裡的意義，例如連續、大小關係等。而為了打破數字間的連續性，可以使用一種稱為One-Hot Encoding的編碼方式：因為總共有三個種類的八哥，我們就用三維向量來表示，每個位置代表「是」（1）或「不是」（0）某種八哥。

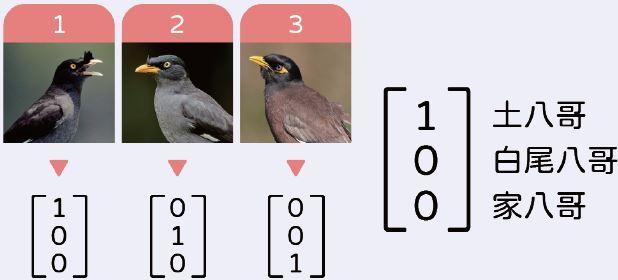
於是，我們的AI模型就會輸出三個數字，分別代表土八哥、白尾八哥、家八哥的得分。

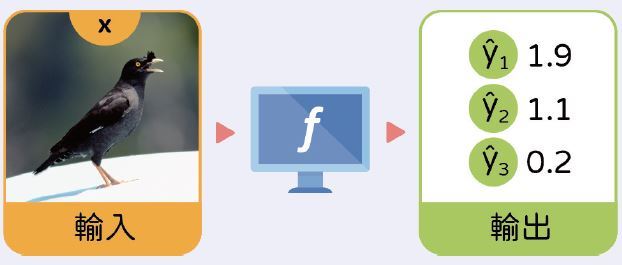
如果訓練成功，只要我們輸入一張照片，會得到三個數字，我們看最高分是誰， 就能夠知道這隻鳥是哪種八哥。比如說輸入一張照片以後，得到的三個分數是1.9、1.1、0.2。因為第一個數字最大，我們就知道這是土八哥！

讓輸出加起來等於1

想想如果現在所有輸出的數字加起來等於1，像是0.7、0.2、0.1，我們就更能清楚的說：「AI 模型告訴我們，這隻鳥有70％的機率是土八哥，20％的機率是白尾八哥，只有10％的機會是家八哥。」感覺是不是能更清楚模型是怎麼「想」的呢？若要做到這樣的AI 模型，我們的問題其實是：「現在有三個數字a、b、c，能不能有個轉換，轉成α、β、γ，保持三者之間的大小關係，且α+β+γ=1？」

我們先看看簡單的版本，如果a、b、c 三個數字都大於0，那就很容易做到這樣子的事。首先，令a、b、c 三個數字的和為S：

S=a+b+c

於是計算a、b、c 佔總和S 的比例，自然就能符合我們的需求。

α=a/S、β=b/S、γ=c/S

現在問題來了：要是a、b、c 中有負的數字，那該怎麼辦呢？我們的第一個想法可能是加絕對值，但這樣子有可能會使小的數字變大。比方說a、b、c原先分別為7、2、-10，原本c 是最小的，但加了絕對值卻會變成最大的數字！

Softmax 神奇的魔術

想要解決上述問題，關鍵是「我們有三個數字a、b、c，你必須想辦法將它們化成三個大於0 的數字a'、b'、c'，但是要保持這三個數字原來的大小關係。」如果能做到的話，就可以用前面的方法，讓三個數加起來等於1。但這該怎麼做呢？

如果把負數變成正數的轉換，想成一個函數。我們其實就是要找一個「永遠大於0，而且是嚴格遞增的函數！」你想得到哪個函數是這個樣子的嗎？當然不只一個函數是這樣，但我們很自然的會想到某個指數函數，例如指數函數的代表，自然指數函數f (x)=e^x。

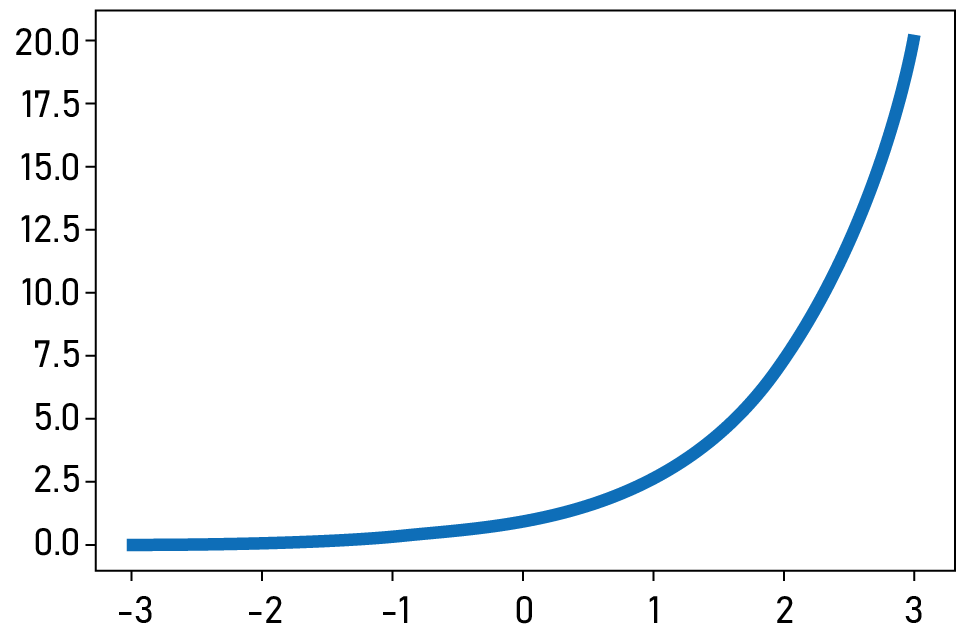
於是a、b、c 就可以轉成大於0 的e^a、e^b、e^c。再經過上一節的方式計算，我們會得到三個看起來有點可怕的公式：

α= e^a / (e^a+e^b+e^c)、β= e^b / (e^a+e^b+e^c)、γ= e^c / (e^a+e^b+e^c)

但仔細看看會發現，這不過就是讓a、b、c 變成大於0 的數，再套用前面的方法使轉換後三個數加起來等於1 嗎？而這種轉換就叫做「softmax」，在人工智慧模型裡是個常用的技巧。

用損失函數衡量我們AI 模型的表現

再來討論一下我們都怎麼幫AI 模型「評分」，一般就是設計一個損失函數（loss function）。簡單來說就是把訓練資料都輸入AI 模型中，讓AI 模型「作答」，最後再看看AI 模型和正確答案的差距大小。而「訓練」就是要想辦法讓這差距變小。

舉例來說，我們有隻土八哥的照片，也就是正確答案是[1,0,0]，而我們的AI 模型算出來的答案是[0.61,0.28,0.11]。由於這兩組數字都可以看成三維空間中的一個點，我們就可以透過計算兩點距離的公式來算誤差：

𝓁=(1-0.61)²+(0-0.28)²+(0-0.11)²=0.2426

這裡要注意的是，原本距離公式是要開根號的，但一來數學家其實很討厭開根號，二來開不開根號，大的數字還是大，小的還是小，所以只是要看誤差是大還是小，開不開根號就無所謂了。而所謂的訓練，就是想辦法調整我們AI 模型的參數，讓損失函數的值愈小愈好。

這樣子計算誤差的方法看起來很合理，但其實有個問題，讓我們用一個例子來說明。假設正確答案是[1,0,0]，而AI 模型輸出是[0.61,0.28,0.11]，此時誤差是前面算過的0.2426。在經過訓練後，AI 模型輸出的答案是[0.61,0.2,0.19]，兩者對於正確的那項都判斷是有61％的機會，對我們來說似乎是一樣好的。不過事實上，訓練前的答案可能會更好一點，至少最不可能的家八哥分數比較低，可是若使用前面的方式計算誤差，會發現後者的損失函數值是0.2282。也就是一個一樣好甚至更好的模型，算出來的誤差值反而比較高！對於這個錯誤的一個想法就是，我們只要專注在正確答案的正確率就好！而在正式討論這件事之前，先來看個很有趣的概念，就是「驚訝指數」。

訊息量和驚訝指數

告訴你一件發生機率比較小的事，訊息量其實是比較大的。比如說在一個幾乎都是晴天的地方，你得到「明天是晴天」這樣的訊息，基本上就是什麼也沒有告訴你；但是如果告訴你「明天是雨天」，那訊息量就變多了。

也就是說，如果有一個訊息是100％會發生的事，那麼有說就和沒說一樣，這時的訊息量是0。因為機率顯然是一個介於0 ～ 1 之間的數字，於是如果我們要定義訊息量，應該是機率愈接近0 愈大，而當機率是1 的時候，訊息量是0。於是當機率是P 時，我們可以定義這看起來很有水準的算式做為訊息量：

𝐥 = -log P

算式很容易檢查，符合我們前面對訊息量的要求。

如果訊息量看來還是有點抽象，你可以想像訊息量就是一個「驚訝指數」。當我們聽到一件發生機率高、很平常的事，當然不太會驚訝。但是聽到一件機率很低的事發生，我們當然就會驚訝萬分，所以訊息量就可以想成是驚訝指數。

平均訊息量就是熵

我們再來看另一個有趣的數字，叫做熵（entropy）。所謂的熵就是指「平均訊息量」或是「平均驚訝指數」。假設有個機率分布P，有三個可能的事件，機率分別是P₁、P₂、P₃。這時相對的訊息量就會是-log P₁、-log P₂、-log P₃。平均訊息量，也就是這個機率分布的期望值就會是：

H(P)= -P₁log(P₁) –P₂log(P₂) –P₃log(P₃)

而平均訊息量大就表示，我們比較難以知道會發生什麼事情，因此有些人會說這個機率分布的「亂度」比較大。亂度也就是我們前面說到的熵。

交叉熵可以當誤差

讓我們回到最前面提到的八哥辨識問題。正確答案P=[P₁,P₂,P₃]=[1,0,0] 我們可以看成一個機率分布，而AI 模型的答案Q=[Q₁,Q₂,Q₃]=[0.61,0.2,0.19]看成是另一個機率分布。這時——前面也說過——我們想專注在「正確答案回答」的狀況。此時如果我們的AI 模型預測土八哥的機率是1，那誤差就是0，而如果預測土八哥的機率愈低，誤差就愈大。這是不是聽來很熟悉？沒有錯，這和我們前面定義訊息量（驚訝指數）的想法是一模一樣的。也就是正確答案是第1 類時，我們希望AI 輸出的-log Q₁ 愈小愈好。如果AI 模型說出正確答案的機率很低，我們就要給它大扣分！

而這個數字就是所謂的交叉熵。在一般兩個機率分布P=[P₁,P₂,P₃]，Q=[Q₁,Q₂,Q₃] 時，交叉熵的定義是：

H(P,Q)= -P₁ log Q₁ –P₂ log Q₂ –P₃ log Q₃

這是用來比較兩個機率分布的方法，可以證明如果P 和Q 的機率分布完全一樣，那麼交叉熵就是最小的；意思就是AI 模型的答案和正確答案一樣的話，數值會是最小的（0）。

聽起來好有學問的KL 散度

最後順便介紹一下，一個聽起來很有學問的KL 散度（Kullback-Leibler Divergence）。假設現在我們有個問題，正確答案可以寫成P 這個機率分布，但我們的AI 模型說是Q。前面說過可以用「最小化」交叉熵H(P,Q)，讓我們的Q 越來越像P。但如果正確答案P 不是One-Hot Encoding 那種形式的話，交叉熵最小就是P 機率分布的熵H(P)。意思是，如果用交叉熵當做我們的損失函數，即使AI 模型完美的和正確答案一樣，損失函數居然也不是0 ！

於是KL 散度就是借用交叉熵的概念，而且讓AI完美回答時損失函數的值，也就是誤差是0。你有想到要怎麼定義這個值嗎？沒有錯，就是交叉熵減去正確答案的熵。

D_KL (P∥Q)=H(P,Q)-H(P)

前面我們學到，當P 和Q 這兩個機率分布完全一樣時，H(P,Q) 是最小的，而且剛好等於H(P)。所以兩個機率分布P、Q 完全相等時，KL 散度D_KL(P∥Q)=0。看完這篇文章，你是不是對人工智慧的演算法又有多一點理解了呢？

延伸學習
將訊息量稱作「驚訝指數」是從這個YouTube影片上看到的。這裡很清楚介紹熵的概念是什麼，非常推薦讀者去看看！
Entropy (for data science) Clearly Explained!!!（StatQuest with Josh Starmer 頻道）