文章專區

突如其來的邀約

1975 年 1 月底，美國布朗大學（Brown University）數學教授班喬夫（Thomas F. Banchoff）下課回到研究室，發現一張助理留下的字條，要他和一位自稱是西班牙畫家達利（Salvador Dali，圖一）的代理人聯絡，並希望他到紐約瑞吉酒店（St. Regis Hotel）與達利見面。當時班喬夫只是位年輕數學家，而達利已是名滿天下的藝術家，班喬夫看了這字條後半信半疑地問了同事意見。「嗯，這要麼是場騙局，要麼會惹來官司，但就算是最壞的狀況，起碼我們有個可以說嘴的好故事。」後來班喬夫決定赴約，最終他見到了達利。

圖一｜西班牙畫家達利（Wikipedia）

原來，《華盛頓郵報》（The Washington Post）在 1 月 22 日刊登一篇專訪，文中介紹了「超立方體」（hypercube，圖二）並附上一張班喬夫手拿展開模型的照片。這引起了達利的注意。

 
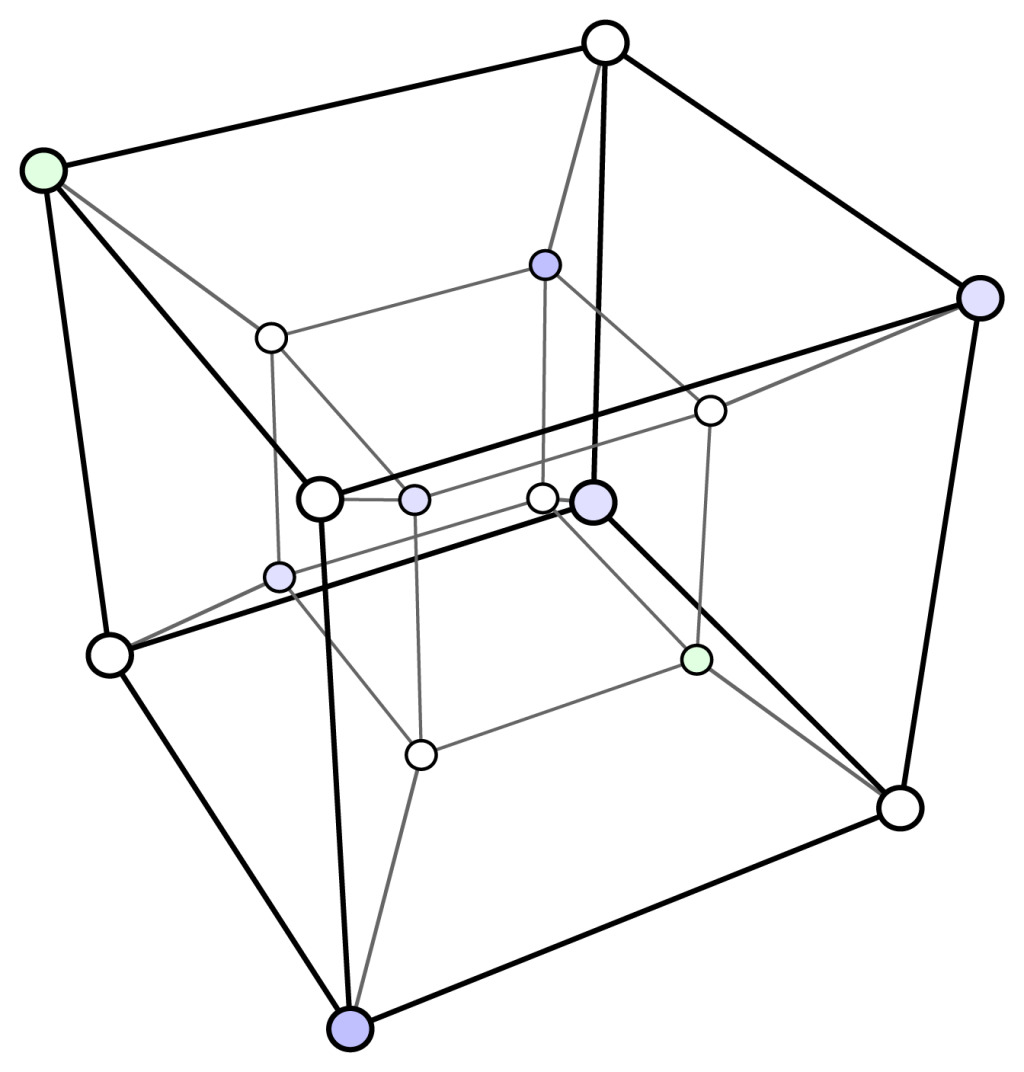
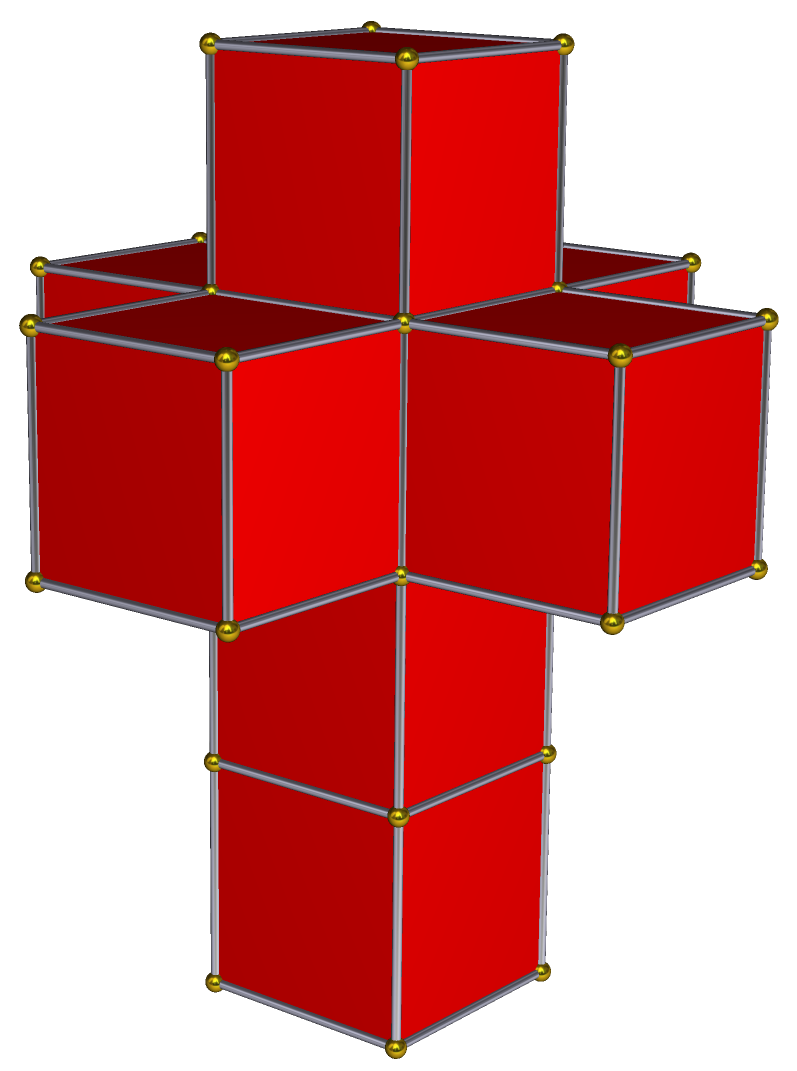
圖二｜超立方體和展開圖（Wikipedia）

20 年的時空邂逅

超立方體，即四度空間中的立方體，展開後是 8個三維正立方體（圖二）。為什麼是 8 個三維正立方體？因為 2 個零維的點可以連成 1 條一維的直線，4 條一維的直線可以組成二維的正方形，6個二維正方形可以組成三維的正立方體，四維的「超立方體」自然由 8 個三維的正立方體組成。

達利早在他的《耶穌受難圖》（Crucifixion，圖三）中以「超立方體」作為十字架的象徵，達利之所以約班喬夫見面，就是希望對方可以讓渡那超立方體模型，以便將它展示於達利當時正在籌備中的博物館。班喬夫一口答應，因為《耶穌受難圖 》就是觸發他往後從事幾何研究的啟蒙動機。班喬夫十歲時在一本漫畫書中首次讀到四度空間，當時的他就被這概念所吸引。1954 年達利創作《耶穌受難圖》，那年班喬夫 16 歲，根據四度空間的類比方式比喻基督教「三位一體」的理論。隔（1955）年，班喬夫初訪紐約大都會藝術博物館（Metropolitan Museum of Art）並親眼見識到《耶穌受難圖》，回去後便在日記本中寫下：「薩爾瓦多・達利的《耶穌受難圖》令人印象深刻。」當時班喬夫還無法意識到，那次與達利作品的邂逅會對他的職業生涯產生什麼影響。

圖三｜（Crucifixion, Salvador Dali）達利《耶穌受難圖》

班喬夫後來進入加州大學柏克萊分校（University of California, Berkeley）博士班就讀，師從華裔數學家陳省身進行幾何學研究。在研究多面體環面（polyhedral tori）性質時，他認識到具有 16 個四邊形的多面體環面，實際上是四維空間中由「超立方體」的正方形所構成環面在三度空間的投影。此時，班喬夫才意識到這種多面體表面與達利《耶穌受難圖》中「超立方體展開模型」之間的連結，於是製作了「超立方體」模型（圖四），也才有後來和達利見面的機會。

圖四｜1973 年班喬夫在加州大學柏克萊分校手拿超立方體展開模型。（Wikipedia）

圖五｜達利《時間的記憶》（The Persistence of Memory, 1931, Salvador Dali ）

達利的神祕宣言

1940～ 1950 年代，當時畢卡索所引領的「立體主義」以藝術解構現實，一時蔚為風尚。達利在 1951 年 4 月發表一篇《神祕宣言》（Mystical Manifesto），文中除感謝畢卡索終結當代繪畫藝術的醜陋之外，更自詡為「新偏執批判神祕主義」的發明者和現代繪畫藝術的救世主，正如他的名字一般（西班牙語中的 Salvador 意為救世主）。他說這種達利神祕主義（Dalian Mysticism）主要依賴於科學的進步，特別是量子物理的實在性所衍生出形而上的精神性（the metaphysical spirituality of the substantiality of quantum physics）。達利舉例，一粒麥子漂浮在離地面一公尺半的空中，會牢牢地固定在那兒，以至於一頭大象用盡全力也無法撼動它；若你掀開海灘上的海水，將會發現睡著一隻活生生的狗。即使這些聽起來不可思議，達利說：「一旦你看到了它們，你就能逼真地描繪它們。」文中，達利又提到愛因斯坦的相對論瓦解了時間的絕對性，激起他的靈感而將時鐘畫得虛軟無力（圖五）。 這種超現實的想像也反映在《耶穌受難圖》中。畫中的耶穌沒有流血，看不見滿臉痛苦哀淒的表情，側仰的臉龐反而顯現出一種引以為傲的無悔。耶穌身上的釘子被立方塊所取代，但並沒有釘在耶穌身上，而是和四度空間的「超立方體」一起飄浮在三度空間中，似乎象徵著耶穌就是時空的主宰。此時，數學與宗教共構出一種難以言喻的矛盾與和諧。……【更多內容請閱讀科學月刊第673期】