文章專區

Take Home Message
• 義大利物理學家伽利略從吊燈的擺盪得到靈感，發現擺盪週期與擺長變化的關聯，但未留下依此原理製作的擺鐘模型。物理學家惠更斯則發明了擺鐘，為機械計時開啟重要里程碑。
• 中國歷史上也曾有許多利用水的流失來計時的工具，稱為「漏刻」或「漏壺」，包括沉箭壺、浮箭壺、蓮花漏等。
• 現代常見的手機中有陀螺儀元件，遵循角動量守恆定律，可測定並穩固方向。

「蹴罷秋千，起來慵整纖纖手。露濃花瘦，薄汗沾衣透。」這是北宋著名詞人李清照在《點絳唇．蹴罷秋千》的詞句，描寫少女剛下秋千後，羅衣微汗、手勢慵懶的模樣。字裡行間可以感受到秋千仍在悠悠擺動，彷彿時間暫停在那一刻的餘韻中。這樣的畫面，不僅詞意盎然，也藏有物理學中「單擺運動」的奧祕。

從擺盪的吊燈到機械時鐘

除了秋千，只要是懸掛物品，迎風擺盪便是常見的經驗。想像在沒有電燈照明的年代，夜晚常需使用燭火，將燭火垂掛的吊燈擺盪並不少見。西方教堂或修道院也有懸掛類似的照明設備，經風吹拂，吊燈就會隨之搖晃。千百年來，不知有多少人在教堂內虔誠地低頭禱告，他們都太專心了，忽略這吊燈擺盪的規律。根據傳言，1583 年義大利物理學家伽利略（Galileo Galilei）在比薩主教座堂（Pisa Cathedral）內祈禱時，不知何故，竟然抬頭觀察吊燈的動態規律，於是一種全新的計時鐘錶概念由此誕生。

伽利略無意間發現擺盪似有規律，而大自然規律的後頭，往往都隱藏了一個自然定律。伽利略當下用自己的脈搏量測吊燈擺盪的週期，也就是吊燈來回擺動的時間。他發現即使擺盪變弱、擺盪幅度變小，擺盪的週期也沒有太大變化，這大大出乎意料，因為當時人們普遍認為當擺盪變弱，擺盪的幅度變小，吊燈擺動的週期時間應該是愈來愈慢，但經過和脈搏的比對，這擺盪的時間並沒有顯著變慢。

這種週期不變的擺盪行為正是鐘錶計時所需要的特性，在伽利略的《論兩種新科學及其數學演化》（Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze）一書當中，他進一步描述擺動的週期與擺的質量、材料無關，而是隨著擺長的平方根變化。也就是說吊燈裡的一支蠟燭和十支蠟燭都有相同的擺盪週期，反倒是愈長的吊繩擺盪得愈久，四公尺的吊繩比一公尺的吊繩慢，週期是原來的兩倍。但這個意外發現並未讓他立即做出單擺鐘，根據記載，1641 年伽利略指導兒子維琴佐（Vincenzo Galilei）和學生維維安尼（Vincenzo Viviani）繪製了擺鐘的圖樣，據說還有模型，但模型因遺失而未留傳後世。1656 年荷蘭物理學家惠更斯（Christiaan Huygens）獨立發明了擺鐘（圖一），並在1657 年獲得專利，成為機械計時的重要里程碑。

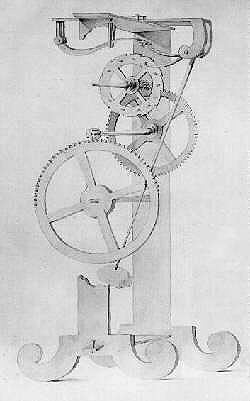
圖一 | 惠更斯設計的機械鐘擺（Wikimedia, Public Domain）

漏水計時與單擺運動的等時性

很可能因為晚年的眼盲，伽利略並沒有將單擺的等時特性應用在自由落體實驗的計時，即便是在斜坡實驗，伽利略使用的也是水鐘的裝置。他在水桶底下挖了個小洞，裝了條小管子，讓水從桶子流經小管子到一個杯子內，藉由乘量杯子內的水重，作為時間流逝的比較。例如以圓球在斜坡上滾動一公尺和兩公尺所流失的水重比例，作為滾動一公尺和兩公尺的時間比例。這種利用水流失的多寡來表示時間流逝的裝置，很類似中國的漏刻。西元六世紀，中國南北朝南梁的《漏刻經》一書記載「漏刻之作，蓋肇於軒轅之日，宣乎夏商之代。」說明這個計時之用的漏刻似乎可追朔到黃帝之遙。

漏刻又稱漏壺，漢代出土的漏壺是種青銅器皿，當中可盛水，以倒立豎箭標示時間，稱為「沉箭壺」或「沉箭漏」。但是漏壺流失的水量會因壺內剩水的多寡而有不同的流失速度，等時性〔註〕不佳。唐代的「浮箭壺」則是外加水到壺內，倒立豎箭可因注水而上浮（圖二）。1030 年，北宋通才燕肅設計了「蓮花漏」，蓮花漏有兩個供水壺，上壺注水較快，下壺有溢水裝置，一旦超過特定水位，多餘的水就會從旁流溢，使得下壺保持固定水位，並將等量的水注入浮箭壺。後來又出現多級漏壺的設計，都是為了時間的等時性，藉此保證時鐘的準確。

〔註〕指每一段時間漏相同的水量。

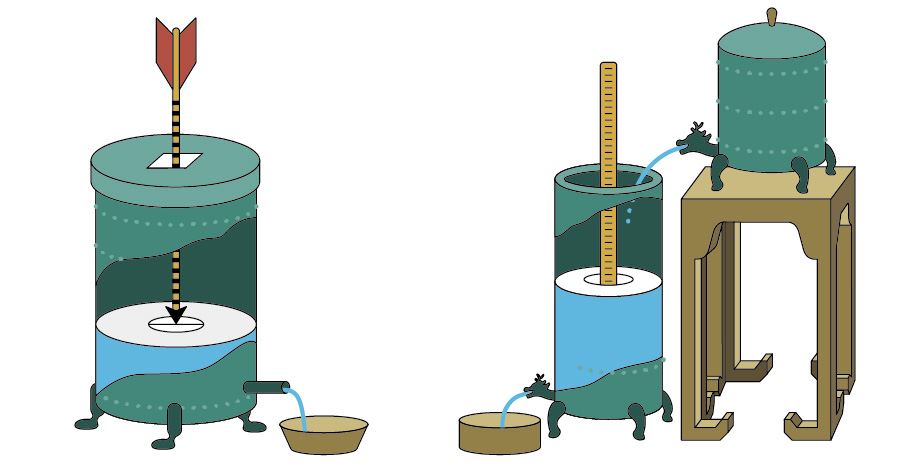
圖二 | 浮箭壺和沉箭壺（黃琳琇繪製）

嚴格說來，單擺唯有在擺幅小於 5 度的時候才具有等時性，當擺幅較大時，就沒有這項特性。也就是說我們若一直拉直擺線，以圓周方式擺動，單擺週期就不定。惠更斯則發現唯有特殊的擺線形式，才能保有單擺的等時性。

單擺以支撐點作為圓心的圓周運動，會受到重力影響，因此在擺盪的過程中受到的向心力不固定，使得不同的擺幅，週期也不同，沒有等時性。而擺線是某種特定形式的幾何線，擺線的向心力一直保持固定常數，這表示單擺若以擺線的形式，則擺動的週期為常數，就像一般的圓周運動一樣，只不過擺線所對應的圓心一直改變。由於擺線的擺動週期為常數，具有等時性，可做為時鐘。……【更多內容請閱讀科學月刊第669期】